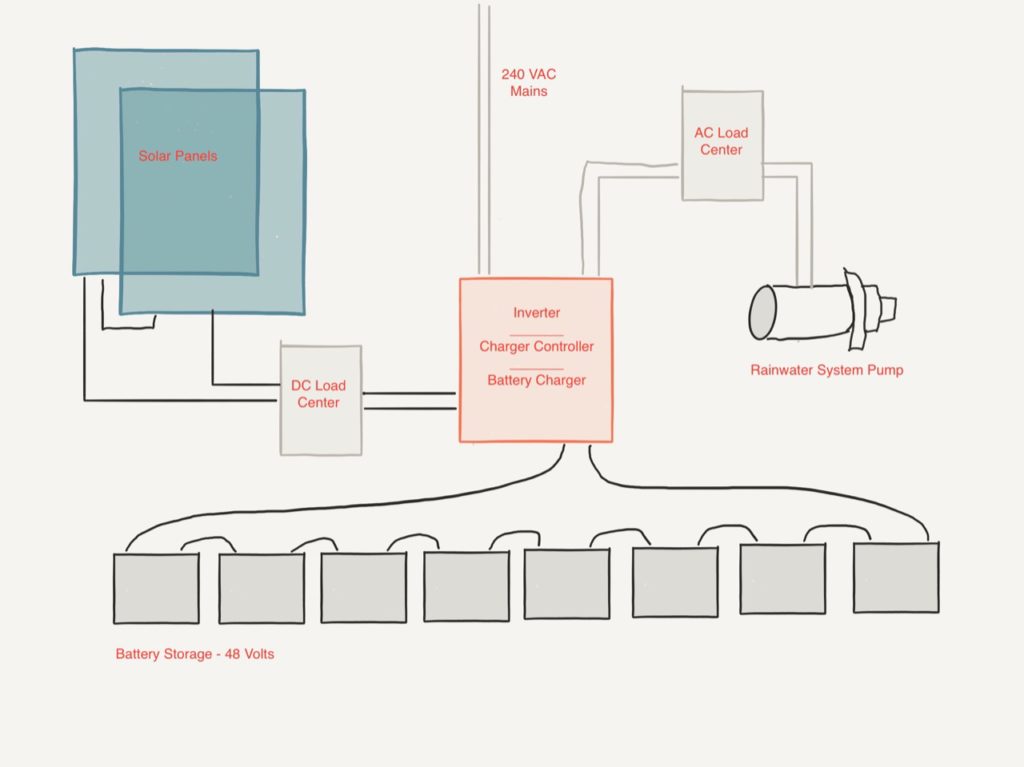
Solar Powered Rainwater Project – Panels, Batteries and Inverters — Oh My!
In a previous Project post, we determined our power needs – 1300 watt-hours per day to pump water. Now we can calculate the battery bank capacity, solar panel wattage, and inverter capacity needed for our installation. Let’s start with the panel wattage. As I mentioned in the last post, the immediate goal is to power a 3/4 horsepower shallow-well pump, with a little power for the ultraviolet filter that cleans the water for house use. The filter uses 30 watts of power, so by multiplying that times 24 hours, we get 720 watt-hours. When added to the pump power consumption of 1300 watt-hours per day, our total is 2020 watt-hours per day. That’s what we have to collect from the sun.
How much sun is hitting the roof each day? Tables on the Internet show the insolation, or amount of solar radiation reaching a given area at various latitudes. The tables show that San Antonio (nearest datapoint to our home) averages 5.3 Kilowatt hours per square meter per day. Unfortunately, insolation varies during the year, and since we want our system to function even in the winter months, we’ll use the low figure for San Antonio of 4.65. That way, we will have plenty of power year around. The final factor is efficiency. No system is 100% efficient, with inverter losses, wire losses and even dirt on the panels playing a factor. It’s safe to assume an efficiency of around 67% for our system. Now we apply the formula to determine panel wattage:
- (Watt-hours/day / insolation) / efficiency = panel wattage.
Inserting our numbers we get: (2020 / 4.65) / .67 = 648 watts of panel collection.
Since we need to pump water around the clock, we’ll have to supply power even when it’s dark. That’s where the batteries come in. There are several variables when figuring the battery bank capacity, including system voltage (12, 24 or 48 volt), watt-hours needed, days of autonomy, inverter efficiency, discharge limit, and temperature compensation. Let’s start with the watt-hours per day and inverter efficiency. We already determined a need for 2020 watt-hours per day for our pump and UV filter, but that will have to be converted from the DC voltage (12, 24 or 48 volts) to AC (120 or 240 volts). Inverters are about 92% efficient, losing about 8% of the applied power in the conversion process. This results in a formula:
- Watt-hours per day / Inverter efficiency = Watt-hours per day of storage
Substituting numbers: 2020 / .92 = 2195 Watt-hours of storage per day
What if the sun doesn’t shine for several days? Here we build in “Days of Autonomy,” or the number of days the system can go without any sun. Three days is about right for our location, but your conditions may vary. Also, temperature can effect battery performance. A battery’s rated capacity is normally stated at 77 degrees Fahrenheit, but the same battery might fall to 80% capacity at 50 degrees. Finally, a battery can be discharged to it’s rated capacity, but only at the cost of drastically reducing it’s life. Normally batteries are only discharged to 50% of their rated capacity to prevent damaging them. Another formula:
- Average daily Watt-hours * Days of Autonomy * Battery Temperature Multiplier / Battery Discharge Limit = Battery Bank Capacity in Watt-hours
Substituting numbers: 2195 * 3 * 1.19 / .5 = 15,672 Watt-hours of storage
Finally, we need to determine the battery bank capacity in Ampere-hours. What system voltage you choose will depend on several factors, but generally speaking higher system voltages (like 24 or 48 volts) are preferred for high-wattage inverters. This is because we gain efficiency in the DC wiring and can buy smaller gauge copper wire to save money. Put another way, higher voltages require lower currents to achieve the same wattage and have lower resistive wire losses. I’m going to set mine up for 48 volts using this formula:
- Battery Bank Capacity in Watt-hours / System Voltage = Battery Bank Capacity in Ampere-hours
Substituting: 15,672 / 48 = 327 Ampere-hours of Battery Bank Capacity.
How many batteries is that? Let’s start by imagining how they might be configured. We could just get four, 12 volt, 327 amp-hour deep-cycle storage batteries, but those are expensive batteries and I would rather use the more commonly available (and cheaper) golf cart batteries. They are typically 6 volt, 190 Amp-hour. Assuming we don’t want to have more than two parallel strings (to reduce trouble with charge equalization) can we get the required capacity? Once again, some formulas:
- Battery Bank Capacity (Ah) / Maximum number of parallel strings = Minimum battery capacity
Substituting: 327 Ah / 2 = 163.5 Ah Minimum battery capacity. Yes. Since the golf cart batteries are 190 Ah, that will work.
Since we need to supply 48 volts, how many batteries will be in series?
- DC System Voltage / Battery voltage = Number of batteries in each series string
Substituting: 48 / 6 = 8 batteries in each series string
Doubling that for two series strings, and we will need 16 total batteries. That’s a lot of lead.
Now we have some idea of solar panels and batteries needed for the project. In the next post, we’ll consider inverters, charge controllers and related equipment.

Pingback:Solar Powered Rainwater Project – to Grid-Tie, or not to Grid-Tie. (that is the question) | Roy Creek Ranch
Pingback:Solar Powered Rainwater Project – Solar Panels Installed! | Roy Creek Ranch
Pingback:Solar Power Rainwater Project – Panels and Angles | Roy Creek Ranch
Pingback:Solar Powered Rainwater Project | Roy Creek Ranch
Pingback:Solar Powered Rainwater Project – Batteries | Roy Creek Ranch
Pingback:Solar Powered Rainwater Project – Final Assembly | Roy Creek Ranch
Pingback:A Solar Upgrade for the Teardrop Trailer | Teardrop Trail